| HOME | HELP | FEEDBACK | SUBSCRIPTIONS | ARCHIVE | SEARCH | TABLE OF CONTENTS |
|
|
| |||||||
| |||||||||
MS 10635 Received 28 January 2000; accepted after revision 17 July
2000.
 |
ABSTRACT |
|---|
 TopAbstract IntroductionMethodsResultsDiscussionReferences |
|---|
|
INTRODUCTION |
|---|
| TopAbstractIntroductionMethodsResultsDiscussionReferences |
|---|
Gravity plays an essential role in terrestrial locomotion. Due to gravity we can hit the ground without losing contact with it. However, because of gravity, work has to be done each step to lift the body even when moving on a level surface. Gravity and the braking action of the ground interact during locomotion with two different energy conserving strategies: the pendular mechanism of walking, up to intermediate speeds, and the bouncing mechanism of running, up to the highest speeds attainable.
In both cases the body undergoes a forward deceleration each step due to the
link between the centre of mass of the body and the point of foot contact on the
ground in front of the centre of mass. This deceleration results in a loss in
kinetic energy: 
Ek,f =
0·5M(V2f,max -
V2f,min), where
M is the mass of the body and Vf,max and
Vf,min, respectively, are the maximum and minimum values of
the forward velocity of the centre of mass of the body attained within each
step.
During a running step, the centre of mass is lowered during the forward
deceleration and raised during the forward acceleration so that both the kinetic
and potential energy changes of the centre of mass are absorbed and restored by
the muscles and tendons. During a walking step, in contrast, the centre of mass
of the body is lowered during the forward acceleration and raised during the
forward deceleration. Therefore the kinetic energy loss can be transformed into
a potential energy increase: Ep = MgSv,
where g is the acceleration of gravity and Sv is the
vertical displacement of the centre of mass within each step. As a consequence,
mechanical energy is largely conserved during walking by the conversion of
kinetic energy into gravitational potential energy and the subsequent recovery
of kinetic energy from the potential energy (Cavagna et al. 1963). This
makes the metabolic energy cost per unit distance during walking at the freely
chosen speed about half that during running (Margaria, 1938). Disregarding
lateral movements (which involve negligible work, Cavagna et al. 1963)
the fraction of the total mechanical energy changes of the centre of mass that
is recovered by the pendular mechanism of walking is:
 |
(1) |
where Wf is the positive work done each step to
reaccelerate the centre of mass from Vf,min to
Vf,max, i.e. to restore the kinetic energy of forward motion
(Ek,f); Wv is the positive work done each
step to increase the potential energy (Ep), during the lift of
the centre of mass (Sv); and Wext is the
positive work actually done each step to maintain the motion of the centre of
mass in the sagittal plane (Cavagna et al. 1976). Wext
equals the sum of the increments in the total mechanical energy of the centre of
mass (Ecm), during a step. In an ideal frictionless pendulum
Ecm would be constant, Wext would be nil and
R would be equal to 1. In walking on Earth R attains a maximum of
0·7 at the optimal speed of 5·5 km
h-1, which is about 1 km h-1 faster than the speed at
which Wext is at a minimum. At slower and faster walking
speeds R decreases. In running, R is close to zero at all speeds.
In order to optimize the recovery of mechanical energy (R), the Ek,f and the Ep curves must be equal in amplitude and opposite in phase, as in a pendulum. A change in gravity leads to a change in the amplitude of the Ep curve, which is proportional to gravity, relative to the Ek,f curve, which is not directly affected by gravity. It follows that in order to maintain the same pendular transfer of mechanical energy, a similar change in amplitude of the Ek,f curve would have to take place. Assuming that the change in Ek,f within each step is an increasing function of the walking speed, independent of gravity, the hypothesis was proposed that the inverted pendulum-like mechanism of energy exchange taking place during walking would be optimized at slower speeds in reduced gravity (Margaria & Cavagna, 1964). This hypothesis and its related implications have been tested experimentally in the present study by measuring, by means of a force platform, the mechanical energy changes of the centre of mass (Wf, Wv and Wext) during walking under conditions of simulated gravity lower and higher than on Earth.
A brief communication on part of this work has been reported previously (Cavagna et al. 1998).
|
METHODS |
|---|
| TopAbstractIntroductionMethodsResultsDiscussionReferences |
|---|
Subjects and experimental procedure
The experiments were made on three adult male subjects (62-63 years, 77-81 kg, 1·79 m, leg length (hip to floor) 0·94 m; 48 years, 92 kg, 1·93 m, leg length 1·03 m; 41 years, 85-86 kg, 1·79 m, leg length 0·92 m). Informed, written consent was obtained from each subject, the studies were performed according to the Declaration of Helsinki, and the procedures were approved by the European Space Agency Safety Committee.
Experiments were performed during the 23rd and 24th European Space Agency parabolic flight campaigns. A simulated gravity of 0·4 g was attained during parabolic flight profiles (Pletser, 1994) in a KC-135 and an A300 Airbus, whereas a simulated gravity of 1·5 g was attained during turns of the A300 Airbus. An aircraft orthogonal frame of reference was defined as follows: the X-axis is parallel to the fore-aft axis of the aeroplane, the Y-axis is parallel to the lateral axis of the aeroplane and the Z-axis is perpendicular to the floor of the aeroplane. Three accelerometers (DS Europe, Milan; with a low pass -3 dB cut-off of 5 Hz) measured simultaneously the X, Y and Z components of the acceleration vector in the aircraft reference frame. Results are given as means ± S.D. unless stated otherwise. In the 0·4 g experiments, during the steps analysed, the acceleration was 3·90 ± 0·35 m s-2 in the Z-direction, 0·01 ± 0·16 m s-2 in the X-direction (n = 81) and 0·05 ± 0·02 m s-2 in the Y-direction (data analysed for Airbus experiments only, n = 31). In the 1·5 g experiments, the corresponding figures were 14·99 ± 0·26 m s-2 in the Z-direction, 0·00 ± 0·14 m s-2 in the X-direction and 0·12 ± 0·17 m s-2 in the Y-direction (n = 101). Since the X- and Y-axis accelerations of the frame of reference were nearly zero, the acceleration along the Z-axis of the frame of reference is equivalent to the vertical on Earth, and the X-Z plane corresponds to the sagittal plane of the subject. Therefore in the following text, forward (or fore-aft), lateral and vertical refer to the X-, Y- and Z-axes, respectively.
During each parabola or turn, the subjects walked at different speeds back and forth across a 3·0 m × 0·4 m force platform fixed to the floor along the X-axis of the aeroplane. The platform (Heglund, 1981) was sensitive to the force exerted by the feet in the forward (X) and vertical (Z) directions; lateral (Y) forces were neglected. The lowest frequency mode of vibration for the unloaded platform was greater than 180 Hz in both the vertical and the fore-aft directions. The simulated gravity was maintained for about 30 s at 0·4 g and 60 s at 1·5 g: during this period the subject could walk several times back and forth on the platform. Two handrails, fixed on each side of the platform, proved to be useful (particularly at 1·5 g) in case the subject lost balance. Four photocells fixed 0·8 m apart at neck height along the side of the platform were used to determine the average walking speed.
Data collection was under the control of a microcomputer. Force platform signals, photocell circuit output and accelerometer signals were digitized at 66-80 Hz at 0·4 g and 50 Hz at 1·5 g, and stored on disk for subsequent analysis. No subject suffered motion sickness and all found walking at 0·4 g easy and comfortable. Walking at 1·5 g required more effort, and any instability tended to quickly result in a loss of balance due to the greater vertical acceleration. At the highest speeds in the 1·5 g experiments, the forward velocity tracings showed that the subjects were still accelerating at the end of the passage, indicating that the speed was limited by the length of the track.
Data were gathered as follows. For the 0·4 g experiments, on the KC-135 aircraft one subject had 6 parabolas, 2·5 min recording time and 50 steps analysed; on the A300 aircraft, the second subject had 4 parabolas, 2 min recording time and 17 steps analysed, and the third subject had 4 parabolas, 2 min recording time and 14 steps analysed. For the 1·5 g experiments on the A300 aircraft, one subject had 3 turns, 3 min recording time and 44 steps analysed; the second subject had 2 turns, 2 min recording time and 27 steps analysed; and the third subject had 2 turns, 2 min recording time and 30 steps analysed. For the 1 g experiments, one subject had 37 steps analysed; the second subject had 26 steps analysed; and the third subject had 20 steps analysed.
Analysis of force platform records and work measurements
The potential and kinetic energy of the whole body, divided unto n segments of mass m, can be measured from the gravitational and the kinetic energy of each segment calculated at each instant of time (t) relative to the frame of reference:
 |
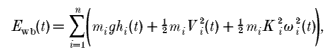(2) |
where Ewb is the mechanical energy of the whole
body; hi and Vi, respectively, are the
height and the linear velocity of the centre of mass of the ith segment
relative to the frame of reference; 
i and Ki,
respectively, are the angular velocity and the radius of gyration of the
ith segment around its centre of mass; and g is the acceleration
of gravity. Equation (2) can be expressed as (Willems et al. 1995):
 |
(3) |
where M is the mass of the whole body; H is the height of the centre of mass relative to the frame of reference; V is the velocity of the centre of mass relative to the frame of reference; and Vr,i is the linear velocity of the centre of mass of the ith segment relative to the centre of mass of the whole body.
The aim of the present study is to determine the mechanical energy changes of the centre of mass of the body resulting from its interaction with the ground during walking at different speeds and gravity values. To this end, only the first two terms of eqn (3) need to be measured, i.e. the gravitational potential energy and the kinetic energy of the centre of mass of the whole body. No attempt was made to determine the total mechanical work done, which would also involve the measurement of the third term of eqn (3) i.e. the internal work necessary to sustain: (i) the changes in the translational kinetic energy of the segments resulting from their speed changes relative to the centre of mass of the whole body, plus (ii) the changes in the rotational kinetic energy of the segments.
The mechanical energy of the centre of mass is equal to the algebraic sum, made at each instant, of the first two terms of eqn (3). The sum of the increments in the resulting curve during a step is called external positive work (Wext), because an external force is necessary to increase the mechanical energy of the centre of mass relative to the surroundings. Using the definition of work, Wext is given by:
Wext(t) =
F(t)s(t) = |F(t)|
|s(t)| cos  ,
= Fv(t)sv(t) + Ff(t)sf(t) + Fl(t)sl(t), = Ep(t) +
Ek,v(t) + Ek,f(t)
+ Ek,l(t) = Ecm(t),
|
(4) |
where the vector F(t) is the resultant of all external
forces exerted at each instant of time t on the body with its projections
in the vertical direction (Fv(t)), forward direction
(Ff(t)) and lateral direction
(Fl(t)); the vector s(t) is the
displacement of the centre of mass of the body with its projections in the
vertical direction (sv(t)), forward direction
(sf(t)) and lateral direction
(sl(t)); and Ep(t), Ek,v(t), Ek,f(t), Ek,l(t) and Ecm(t) are,
respectively, the changes in gravitational potential energy, kinetic energy of
vertical motion, kinetic energy of forward motion, kinetic energy of lateral
motion and total mechanical energy of the centre of mass. Since the work
necessary to sustain the lateral displacements is negligible (Cavagna et
al. 1963), we have measured only the mechanical energy changes of the centre
of mass associated with its trajectory in a sagittal plane (Fig. 3).
During walking on the level at a constant speed, the velocity (and as a consequence the kinetic energy) and the height (and as a consequence the potential energy) of the centre of mass of the body are equal at the beginning and end of each step. This means that, during the step, the increments in the mechanical energy of the centre of mass must equal the decrements. When the mechanical energy of the centre of mass increases, positive external work is done by the muscular force; when the mechanical energy of the centre of mass decreases, negative external work is done by the muscular force and external friction. Since during walking the negative work done by external frictional forces is small, the negative external work done by the muscular force during each step practically equals the external positive work done. It follows that the net work done (positive plus negative) is nil. This is in contrast with some exercises, such as cycling and swimming, where the negative work done by external friction practically equals the positive work done by the muscular force; in this case the muscular force does net positive external work against external friction.
A net external work done by the muscular force equal to zero indicates that the mechanical energy absorbed during negative work equals the mechanical energy delivered during positive work. If all the mechanical energy absorbed during negative work could be stored within the muscles and tendons and subsequently recovered completely as positive work, the energy expenditure to maintain the motion could in principle be zero. A perfectly elastic body would continue to bounce endlessly with no energy input required. However, the mechanical energy stored during the negative work (and subsequently recovered during positive work) is only a fraction of the total mechanical energy absorbed: a substantial fraction, differing according to the amplitude and the velocity of the movement, is dissipated as heat. It follows that mechanical energy must be added during positive work to maintain the movement. This is accomplished by the transformation of chemical energy into mechanical positive work by the contracting muscles. In addition, the muscles must be active also during negative work to develop the force necessary to check the movement. As a consequence energy expenditure takes place during both positive and negative work. It follows that even if the net work done during a step cycle is nil, it is important to determine the work done because it implies an expenditure of energy, i.e. a different internal state of the system from the beginning to the end of the step.
Furthermore, the mechanical energy fluctuations of the centre of mass taking place during a step provide useful information about the mechanisms used to move during steady-state locomotion on the level. In fact, they result from the amplitude, time relationship, and exchange of the potential and kinetic energy of the centre of mass, which differ according to the exercise (e.g. walking vs. running), the speed of locomotion and, as will be described below, the gravity level.
Neglecting air resistance, Fv(t) and
Ff(t) are measured during walking by means of a force
platform sensitive to the fore-aft and vertical components of the force exerted
on it by the subject's feet (Fig. 1). The
platform records were used to determine Ep(t), Ek,v(t), Ek,f(t) and Ecm(t), as
described in detail previously (Cavagna, 1975; Cavagna et al. 1983) and
summarized below.
An example of the experimental tracings obtained during a passage over the platform at a walking speed of about 3 km h-1 during a parabola simulating Martian gravity (0·4 g) is shown in Fig. 1. The upper panel shows the vertical and fore-aft components of the recorded acceleration; the lateral component was less than the fore-aft and is not shown. The middle panel shows the vertical and fore-aft components of the force exerted on the platform by the subject during about four complete steps. The bottom panel shows the output of the four-photocell circuit indicating the mean walking speed in proximity to the chosen step (see below). The direction of movement can be inferred from the change in amplitude of the photocell signal, which corresponds to the photocell number. The vertical dashed lines delimit the step chosen for the analysis described in Fig. 2.
 |
View larger version [in this window] [in a new window] | |
|
The upper panel shows the vertical (av) and fore-aft (af) components of the acceleration recorded during one parabola of the KC-135 aircraft; the lateral component was less than the fore-aft component, and is not shown. The middle panel shows the vertical (Fv) and fore-aft (Ff) force exerted by the subject on the force platform during one passage. The vertical dashed lines delimit the time interval corresponding to the duration of the one step analysed in Fig. 2. The bottom panel shows the output of the photocell circuit; the amplitude of the signal corresponds to the photocell number when the subject interrupted the light beam, indicating the subject's speed and direction. The offsets in the force traces, clearly seen at the beginning and the end of the trial when the subject is not on the platform, are due to the suspended mass of the force plates times the changes in the aeroplane acceleration (traces above). As described in Methods, these offsets were automatically corrected during the analysis using the accelerometer records. Subject mass 77 kg, walking at a speed of 3 km h-1. | ||
 |
View larger version [in this window] [in a new window] | |
|
The two top panels show, expanded, the vertical and fore-aft force during the step indicated in Fig. 1. The subject mass (M) times the simulated gravity (av) was subtracted from the vertical force (Fv) measured by the force platform, so that the signal above and below zero is proportional to the net vertical acceleration of the centre of mass of the subject. The fore-aft force in this passage is positive when the push against the platform is directed forward causing a deceleration of the centre of mass. The third panel shows the forward velocity obtained from the integration of the fore-aft force (hatched areas under the Ff curve) and evaluating the integration constant from the photocells signal. The fourth panel shows the vertical velocity, obtained from the integration of the vertical force minus the body weight (hatched areas under the Fv - Mav curve) assuming the integration constant is equal to zero. The bottom panel shows the vertical displacement of the centre of mass obtained from the integration of the vertical velocity (hatched areas under the Vv curve). The mechanical energy traces, such as those shown in Fig. 3, are calculated from the velocity and vertical displacement of the centre of mass as explained in the text. | ||
The beginning and end of the selected steps were delimited on the basis of the vertical and fore-aft tracings of the platform. A complete step cycle was detected when these tracings repeated their trend (see Fig. 1). Steps were chosen for the analysis on the basis of the regularity of the force-time tracings and of the records of four photocells indicating obvious velocity changes.
The base lines of the vertical and fore-aft force platform records were corrected at each instant for any changes in the acceleration measured by the accelerometers along the Z-and X-axis of the reference frame. During the selected steps, the difference between the mean force measured by the force platform on the Z-axis and the subject's body weight (subject mass × 0·4 g or 1·5 g) was -1·56 ± 10·06 N (n = 81) at 0·4 g and -19·24 ± 32·83 N (n = 101) at 1·5 g. The mean force measured on the X-axis was -0·05 ± 13·57 N (n = 81) at 0·4 g and 0·14 ± 12·97 N (n = 101) at 1·5 g. In the calculation of the velocity changes from the force (see below), these values were all made to be zero, and any ensuing error was neglected. In other words, records in which the subject had a net fore-aft acceleration (on the X-axis) or a net vertical displacement (on the Z-axis) within the selected step were analysed assuming the mean forward acceleration and the net vertical displacement were nil. The errors resulting from this assumption are random and increase the dispersion of the data (indicated by the standard deviation in Figs 4, 5 and 6), but do not affect the conclusions reached in the present study. This was tested by selecting a subset of the data in which the difference between mean force measured by the platform on the Z-axis and the subject's body weight was less than 20 N at 0·4 g and 60 N at 1·5 g, and the net mean force measured by the platform on the X-axis during a step cycle was less than 20 N. In this subset of data the difference between mean force measured by the platform on the Z-axis and the subject's body weight became -2·63 ± 7·95 N (n = 64) at 0·4 g and -13·04 ± 23·03 N (n = 79) at 1·5 g, and the mean force measured on the X-axis was 1·95 ± 8·55 N (n = 64) at 0·4 g and -0·68 ± 7·3 N (n = 79) at 1·5 g. This subset of data resulted in a smaller dispersion of the data (as indicated by the smaller S.D.) having the same average trend shown by all the data in Figs 4, 5 and 6. We therefore used all the originally selected data.
An example of the procedure used to determine the velocity and vertical displacement of the centre of mass from the force records is shown in Fig. 2. The two top panels show the vertical and fore-aft force during the step selected in Fig. 1, on a greatly expanded time scale. The vertical force oscillates around the body weight (about 300 N at 0·4 g). When the push against the platform is directed forward relative to the subject, the fore-aft signal of the platform can be either positive or negative depending upon the direction of walking for a particular trial. For example, in the passage shown in Figs 1 and 2, the positive signal from the platform corresponded to a forward push, causing a deceleration of the centre of mass of the subject.
The forward velocity is shown in the third panel. It was obtained from the integration of the fore-aft force curve (hatched areas in the second panel of Fig. 2) and by evaluating the integration constant as the mean forward speed calculated from the photocell signals. This procedure may involve errors if the mean forward speed measured by the photocells is not equal to the mean forward speed of the centre of mass. For example, the moving limbs can interfere with the photocell beams, but this was avoided by placing the photocells at the level of the neck. Even so, errors can arise because the forward velocity of the centre of mass of the body differs from the forward velocity of the neck. However, the forward displacement of the centre of mass within the trunk during walking on Earth is less than 2 cm (Fig. 12 of Cavagna et al. 1963), and since the distance between photocells was 80 cm, the maximum error would be 2·5 %. Errors due to the tilting of the trunk during walking on Earth are of the same order of magnitude, and would tend to diminish rather than increase the error due to movement of the centre of mass within the trunk (N. Heglund, unpublished observations). All these possible errors are random rather than systematic and were neglected.
The vertical velocity is shown in the fourth panel of Fig. 2. It was obtained from integration of the vertical force signal minus the body weight (hatched areas in the top panel). The integration constant was set to zero on the assumption that the net vertical displacement was nil (Cavagna, 1975; Cavagna et al. 1983), i.e. that the mean vertical force during the step period was equal to the body weight. The error resulting from this assumption is discussed above. The vertical displacement of the centre of mass is shown in the bottom panel. It was obtained from the integration of the vertical velocity curve (hatched areas in the fourth panel).
The kinetic energy of forward motion (upper curve in each panel of Fig. 3) was calculated as: Ek,f = 0·5MVf2, from the mass of the body (M) and the instantaneous forward velocity of the centre of mass (Vf), as shown in Fig. 2. The gravitational potential energy (dotted middle curve in each panel of Fig. 3) was calculated as: Ep = MgSv, where g is the recorded vertical acceleration during the step (Fig. 1) and Sv is the vertical displacement of the centre of mass during the step, determined as shown in Fig. 2. The small kinetic energy of vertical motion, Ek,v = 0·5MVv2, calculated from the vertical velocity of the centre of mass (Vv in Fig. 2), was added to Ep to obtain the mechanical energy changes of vertical motion of the centre of mass (continuous middle curve in each panel of Fig. 3, barely distinguishable from the Ep curve). The total mechanical energy of the centre of mass (Ecm) was calculated by summing at each instant Ek,f and Ep + Ek,v; this procedure allows an energy exchange between gravitational potential energy and kinetic energy of the centre of mass.
The positive work done during the step to reaccelerate the body (Wf) was calculated as the sum of the increments in the Ek,f curve; the positive work done to lift the body against gravity (Wv), was calculated as the sum of the increments of the (Ep + Ek,v) curve; and the positive work done to maintain the movement of the centre of mass in the sagittal plane (Wext), was calculated as the sum of the increments of the Ecm curve (bottom curve in each panel of Fig. 3).
|
RESULTS |
|---|
| TopAbstractIntroductionMethodsResultsDiscussionReferences |
|---|
The mechanical energy changes of the centre of mass taking place during the step at equivalent walking speeds (i.e. speeds with similar pendular recovery of mechanical energy, R) are shown in Fig. 3 for 0·4, 1·0 and 1·5 g. Data at 1·0 g were obtained from earlier studies on the same subjects, who have been giving consistent results over many years (Cavagna et al. 1983; Willems et al. 1995); furthermore these results are equivalent to those determined on many other subjects in previous studies (Cavagna et al. 1976; Cavagna et al. 1983; Willems et al. 1995).
 |
View larger version [in this window] [in a new window] | |
|
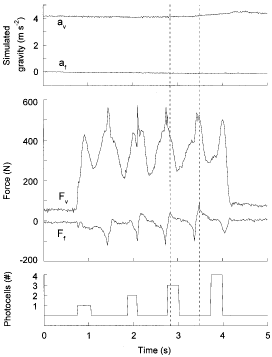
The mechanical energy changes of the centre of mass of the body during one step of walking at low speeds (upper row), intermediate speeds (middle row) and high speeds (lower row) are shown for a simulated gravity of 0·4 g (left column), 1·0 g (middle column) and 1·5 g (right column). In each panel, the upper curve shows the kinetic energy of forward motion of the centre of mass (Ek,f); the middle curve shows the gravitational potential energy (Ep, dotted line) and the sum of the kinetic energy of vertical motion of the centre of mass (Ek,v) plus Ep (continuous line); and the lower curve shows the total mechanical energy of the centre of mass (Ecm = Ek,f + Ek,v + Ep). In each panel the speed of walking and the pendular recovery of mechanical energy (R) are indicated. Each row shows tracings recorded at roughly equivalent speeds (i.e. with similar R) for the different gravity levels; note the similar shape of the traces in each row and that the equivalent speeds are greater the higher the gravity. | ||
In each panel of Fig. 3, the upper trace shows the kinetic energy of forward motion of the centre of mass (Ek,f); the middle traces show the gravitational potential energy (Ep, dotted line) and the sum of the kinetic energy of vertical motion of the centre of mass (Ek,v) plus Ep (continuous line); and the lower trace shows the total mechanical energy of the centre of mass (Ecm = Ek,f + Ek,v + Ep). The upper panels show tracings obtained at slow speeds of walking where the recovery (R) is less than the maximum. The middle panels show tracings obtained at speeds where R is at the maximum. The lower panels show tracings obtained near the fastest speeds reached; no such tracings could be consistently obtained at 1·5 g due to the limited length of the track.
At the speed for a maximum R, the Ek and Ep curves had similar amplitude and were nearly in opposition of phase within each gravity class; furthermore, the condition for an optimal R occurred at a walking speed that increased with gravity. On the other hand, at a given absolute speed (e.g. at 5·4 km h-1 at 0·4 and 1·0 g) the mechanical energy changes increased with increasing gravity.
At low speeds (top panels in Fig. 3) the gravitational potential energy changes were larger than the kinetic energy changes, with the consequence that the shape of the Ecm curve is similar to the shape of the Ep + Ek,v curve. On the contrary, when the walking speed increased above the speed at which R is at a maximum, the kinetic energy changes increased relative to the potential energy changes (bottom panels in Fig. 3). In this case, the Ecm curve became similar to the Ek,f curve. The increasing amplitude of the Ecm curve indicates that the muscles play an increasingly greater role. The fastest speed reached was greater at 1·0 g than at 0·4 g. At both slow and fast walking speeds R was less than at intermediate speeds (as indicated in each panel), since an optimal pendular transfer requires the same amplitude in the two curves.
The positive work done per unit distance to sustain the forward speed changes (Wf) and the gravitational potential energy changes (Wv) of the centre of mass, calculated from the sum of the increments in the Ek,f and (Ep + Ek,v) curves, are plotted in Fig. 4 as a function of walking speed for 1·5, 1·0 and 0·4 g. The three panels in Fig. 4 show that, at any given speed, both Wf and Wv increased with increasing gravity, as could be inferred from the increasing amplitude of the mechanical energy curves in Fig. 3. Furthermore, Wf increased linearly with speed with a slope that was about 40 % greater at 1·5 g and 30 % smaller at 0·4 g, than at 1·0 g.
 |
View larger version [in this window] [in a new window] | |
|
The weight specific work done per unit distance against gravity
(Wv; | ||
At 1·5 and 1·0 g, Wv increased with speed to a maximum and then decreased, whereas at 0·4 g it remained about constant and then decreased with speed. The relative increase in Wv with speed was two times larger at 1·5 g than at 1·0 g. As described by Coates & Meade (1960), the increase in the vertical displacement of the centre of mass with speed at 1·0 g is associated with an increase in the step length. In fact, the centre of mass is at its lowest when the angle between the two legs is greatest, and is at its highest when the angle is approximately zero. Therefore the longer the step length, the greater would be the vertical excursion of the centre of mass. However, an extension of the ankle of the foot about to leave the ground takes place when the feet are maximally apart and the centre of mass is falling forward, approaching its lowest point. With increasing speed, this extension becomes more vigorous and its vertical component tends to oppose the lowering of the centre of mass, which is consequently reduced. When the vertical component of the push is greater than the body weight, the centre of mass is lifted also in this phase of the step (Cavagna & Margaria, 1966). This mechanism may explain the decrease in Wv at high walking speeds in all gravity classes. It is possible that in reduced gravity, the extension of the ankle has a greater effect in lifting the body while it is falling forward, and that this completely masks the effect of the increasing step length in increasing Wv.
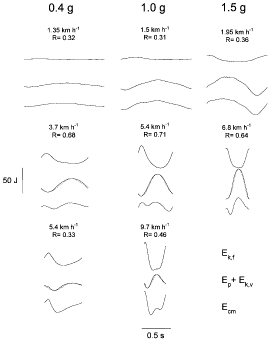
The speed at which Wv and Wf became equal, i.e. the speed at which the two lines in each panel of Fig. 4 cross, increased with gravity. As mentioned above, in order to attain the maximum recovery (R), it is necessary to have Wv = Wf and a 180 deg phase difference between the Ep and Ek,f curves. Due to this pendular recovery of energy, the mechanical work actually done by the muscles to maintain the movement (Wext) is smaller than Wv + Wf. Both R and Wext are plotted in Fig. 5 as a function of walking speed for the three gravity values. R attained a maximum near 3·5 km h-1 at 0·4 g, 5·5 km h-1 at 1·0 g and possibly 6·5 km h-1 at 1·5 g (see Discussion). The maximum value of R seemed on average to be lower at 0·4 g (0·55) and 1·5 g (0·60) than at 1·0 g (0·70). On the other hand, Wext attained a minimum of 0·15 J kg-1 m-1 near 2·5 km h-1 at 0·4 g, a minimum of 0·30 J kg-1 m-1 near 4·5 km h-1 at 1·0 g, and maintained a lowest value of 0·60 J kg-1 m-1 up to about 4·5 km h-1 at 1·5 g. At 0·4 g, the minimum of Wext was one-half that on Earth whereas at 1·5 g it was two times greater.
 |
View larger version [in this window] [in a new window] | |
|
The energy recovered via the pendular exchange between gravitational potential energy and kinetic energy of the centre of mass of the body (left panels) attains a maximum at a walking speed that increases with gravity. The arrows indicate the speeds for an optimal recovery predicted by the model shown in Fig. 7. The right panels show the work done per unit distance to maintain the movement of the centre of mass in the sagittal plane (Wext). Note the intercept and scale differences on the Wext ordinate. Wext attains a minimum at a speed slightly slower than the speed at which recovery is at a maximum. The symbols represent mean values (n is given by the number near each symbol in the right panels) of the data collected in three subjects as follows. For the 0·4 g experiments: one subject had 6 parabolas, 2·5 min recording time and 50 steps analysed; the second subject had 4 parabolas, 2 min recording time and 17 steps analysed; the third subject had 4 parabolas, 2 min recording time and 14 steps analysed. For the 1·5 g experiments: one subject had 3 turns, 3 min recording time and 44 steps analysed; the second subject had 2 turns, 2 min recording time and 27 steps analysed; the third subject had 2 turns, 2 min recording time and 30 steps analysed. For 1 g experiments: one subject had 37 steps analysed; the second subject had 26 steps analysed; and the third subject had 20 steps analysed. The data are grouped into the following intervals along the abscissa: < 1·08, 1·08 to < 1·44, 1·44 to < 1·80, 1·80 to < 2·16, 2·16 to < 2·52, 2·52 to < 2·88, 2·88 to < 3·24, 3·24 to < 3·60, 3·60 to < 3·96, 3·96 to < 5·04, > 5·04 km h-1 for 0·4 g; < 1·80, 1·80 to < 2·52, 2·52 to < 3·24, 3·24 to < 3·96, 3·96 to < 4·32, 4·32 to < 4·68, 4·68 to < 5·04, 5·04 to < 5·40, 5·40 to < 5·76, 5·76 to < 6·48, 6·48 to < 6·84, 6·84 to < 7·56, 7·56 to < 9·00, > 9·00 km h-1 for 1·0 g; < 2·0, 2·0 to < 2·5, 2·5 to < 3·0, 3·0 to < 3·5, 3·5 to < 4·0, 4·0 to < 4·5, 4·5 to < 5·0, 5·0 to < 6·0, 6·0 to < 7·0, 7·0 to < 8·0, > 8·0 km h-1 for 1·5 g. Bars indicate the standard deviation of the mean when they exceed the size of the symbol. Lines represent the weighted mean fit of all the data (KaleidaGraph 3.08d). | ||
At 0·4 and 1·0 g the minimum Wext was attained at a speed slightly slower than the speed for a maximum of R. This difference is probably due to the fact that the sum Wv + Wf increases with speed after Wext is at a minimum. According to eqn (1) this may result in a slight additional increase of R with speed in spite of the fact that Wext begins to increase.
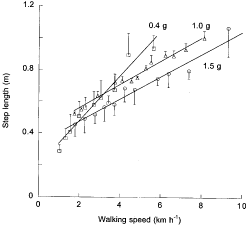
A two factor ANOVA (SuperANOVA version 1.11) was performed to quantify the effect of speed and gravity on Wf, Wv, Wext, R and the step length (Fig. 6) during walking. For all variables the effect of speed and gravity were statistically significant (P < 0·001).
 |
View larger version [in this window] [in a new window] | |
|
Step length is shown as a function of speed at 0·4 g ( | ||
|
DISCUSSION |
|---|
| TopAbstractIntroductionMethodsResultsDiscussionReferences |
|---|
Walking speed range and total mechanical work
The present results show that the greater external work done during walking at high gravity values is accompanied by an increased range of speeds that can be maintained with the mechanism of walking. In fact, the speeds at which Wf = Wv (Fig. 4), Wext is at a minimum and R is at a maximum (Fig. 5), all increase with gravity. Also the step length attains a maximum of about 1 m at a speed which increases with gravity: 5·7 km h-1 at 0·4 g, 8·0 km h-1 at 1·0 g and 9·5 km h-1 at 1·5 g (Fig. 6).
The external work required to walk a given distance is significantly greater at higher gravity (Fig. 5). The internal work done per unit distance, which is the work required to reset the limbs relative to the centre of mass of the body (i.e. the sum, each step, of the increments in the third term in eqn (3)), increases with step frequency (Cavagna & Franzetti, 1986). The internal work done per unit distance is therefore likely to be independent of gravity or to increase with increasing gravity, due to the fact that the step length, at a given speed, is about the same or decreases with increasing gravity (Fig. 6). It follows that at all speeds the total work done during walking, the sum of the external work plus the internal work, will probably be greater the higher the gravity.
Relation to previous studies
A decreased work of walking at 0·4 g relative to 1·0 g is consistent with the decreased metabolic energy consumption reported during walking in reduced gravity simulators (Fox et al. 1975; Farley & McMahon, 1992; Newman & Alexander, 1993; Newman et al. 1994). A decrease in the walking speed range in reduced gravity was predicted both theoretically and experimentally using partial gravity simulators (Margaria & Cavagna, 1964; Hewes et al. 1966; McMahon, 1984; Davis & Cavanagh, 1993; Newman et al. 1994; Kram et al. 1997).
Rajulu et al. (1992) found, during parabolic flight manoeuvres, that the vertical and fore-aft forces exerted on a force platform decreased with decreasing gravity, and that the fore-aft to vertical force ratio increased with decreasing gravity. These results are consistent with the mechanical work measurements of the present study. Margaria & Cavagna (1964) assumed that the kinetic energy changes of the centre of mass were not affected by a change in gravity, thus leading to an imbalance between kinetic energy changes and potential energy changes. This imbalance was then thought to cause a reduction of the speed of walking in reduced gravity, a conclusion qualitatively similar to that reached here. The present experiments, however, show that kinetic energy changes do in fact decrease with decreasing gravity (Fig. 4), as also found by Griffin et al. (1999) using a suspension reduced-gravity simulator.
Griffin et al. (1999), who found a figure of external work done at 0·5 g consistent with the results of the present study, wondered why the metabolic cost is only reduced by one-quarter when the external work is reduced by one-half at 0·5 g. This is probably due to the fact that the external work is not the only source of metabolic energy expenditure, and that the internal work done to move the limbs relative to the centre of mass must also be taken into account. On Earth, at about 3 km h-1, the internal work approximately equals the external work (Willems et al. 1995). It follows that a reduction to one-half of the external work, with similar internal work (see above), may simply explain the finding that the metabolic cost at 0·5 g is reduced by only one-quarter.
Why does gravity affect the optimal speed of walking?
The optimal walking speed is defined as the speed where R attains a maximum value; this speed is lower at 0·4 g and probably greater at 1·5 g than at 1·0 g. This optimal speed, and why it changes with gravity, can be predicted by the following model based on two factors which cause a forward deceleration each step: the action of gravity during the lift of the body and the impact against the ground at heel strike.
During the time of single contact, the centre of mass is lifted and lowered
while pole vaulting on the link to the point of contact of the foot with the
ground without support by the other leg. When the centre of mass is lifted
during the time of single contact, the kinetic energy of forward motion is
transformed, in part, into gravitational potential energy: the forward speed
decreases from a higher value before the lift, to a lower value after the lift
because of the action of gravity during the lift. The greater the gravity, the
greater will be the deceleration forwards. Although muscular activity is
necessary to stabilize the supporting joints, no muscular activity would be
required to lift the body if the increase in gravitational potential energy
equals the decrease in kinetic energy of forward motion. The forward velocity
change necessary to account for this decrease in kinetic energy (Vgravity) has been calculated
as indicated in the left inset of Fig. 7 and is
shown in the same figure as a function of speed for the three gravity values
(see Appendix).
 |
View larger version [in this window] [in a new window] | |
|
The forward velocity change of the centre of mass of the body due to
the impact against the ground ( | ||
At the moment of heel strike, the velocity of the centre of mass is directed
forward and downward. At the end of the subsequent period of pendular transfer
of kinetic energy into potential energy (the middle of the single foot contact
phase), the velocity of the centre of mass is directed horizontally. This change
in the direction of the velocity vector is due to the link connecting the centre
of mass to the point of contact on the ground. The component of the velocity of
the centre of mass directed along this link at the moment of heel strike is the
'ground component' (Fenn, 1930). The ground component can be resolved into a
vertical component and a horizontal component (right inset in Fig. 7). The
horizontal component (Vground) represents the
fraction of the speed available for raising the centre of mass passively
(Appendix).
The speeds at which Vground equals Vgravity are similar to the
speeds at which R attains a maximum (arrows in Figs 5 and 7), indicating
that the speed change available just equals the speed change required to lift
the centre of mass. In other words, the maximum pendular transfer of energy
occurs when body geometry and speed after heel strike translate into a velocity
change which is equal to the one caused by body geometry and gravity during the
lift in the single foot contact phase.
At speeds slower than the optimal speed Vground < Vgravity. The difference
between Vground
and Vgravity
must be made up by the muscles in order to complete the lift of the centre of
mass. In other words, gravity tends to cause a forward speed change that is
larger than necessary to accommodate Vground. On the contrary, at
speeds faster than the optimal speed, Vground > Vgravity, and the excess speed
change due to the link results in energy absorbed by the muscles. Vground is similar at 1·0 and
1·5 g over the whole speed range whereas at 0·4 g Vground increases with speed
more steeply due to a steeper increase in the step length (Fig. 6).
The Vground
shown in the right inset of Fig. 7 was
calculated from the equation:
Vground =
(Vfc2 +
Vvc2)½cos[
/2 - L/(2lleg)
- arctan(|Vvc|/Vfc)]sin[L/(2lleg)],
where Vvc and Vfc are, respectively, the vertical and forward components of the velocity of the centre of mass at the instant of foot contact (Vc in the right inset of Fig. 7), L is the step length (Fig. 6) and lleg is the average leg length (0·963 m).
The following relationships were calculated as a function of walking speed (Vf) using a least squares linear fit of experimental data (see below):
Vfc,0·4 g = -0·007 + 1·069Vf (r = 0·998, n = 81)
Vvc,0·4 g = -0·026 - 0·097Vf (r = 0·539, n = 81)
L0·4g = +0·196 + 0·507Vf (r = 0·874, n = 81)
Vfc,1 g = -0·036 + 1·077Vf (r = 0·997, n = 84)
Vvc,1 g = -0·046 - 0·068Vf (r = 0·468, n = 84)
L1 g = +0·413 + 0·263Vf (r = 0·964, n = 84)
Vfc,1·5 g = -0·005 + 1·062Vf (r = 0·997, n = 101)
Vvc,1·5 g = -0·022 - 0·170Vf (r = 0·702, n = 101)
L1·5 g = +0·334 + 0·252Vf (r = 0·862, n = 101),
where the velocity is expressed in metres per second and the length in metres, and r is the correlation coefficient.
Vgravity has
been calculated (as indicated in the left inset of Fig. 7) assuming
that the kinetic energy change, Ek,f 
mVgravityVf,
equals the potential energy change, Ep = mgSv,
where m is the body mass, and Sv =
lleg -
llegcos[Lsc/(2lleg)] (see
eqn (2) and Fig.
6 of Cavagna et al. 1976) and is taken as the vertical displacement
of the centre of gravity moving the horizontal distance Lsc
during the time of single contact. It follows that Vgravity =
(glleg/Vf){\123}1 -
cos[Lsc/(2lleg)]}, g was taken as
9·81 m s-2 for 1·0 g, 3·90 m
s-2 for 0·4 g and 14·99 m s-2
for 1·5 g (the last two figures refer to the mean vertical acceleration
measured by the accelerometer during the steps analysed). Data of L,
Lsc, Vfc and Vvc refer to
the present study for 0·4 and 1·5 g, and to previous studies for 1·0
g (Cavagna et al. 1983; Cavagna & Franzetti, 1986; Willems
et al. 1995). The maximal speed at 1·0 g was limited to 8 km
h-1 because the inverted pendulum model only holds up to this speed
(Cavagna & Margaria, 1966; Cavagna et al. 1976).
Lsc, as well as Vfc and
Vvc above, were determined from the characteristics of the
force and velocity tracings (see, for example, Fig. 3 of Cavagna
& Margaria, 1966):
Lsc,0·4g = 0·119 + 0·467Vf (r = 0·882, n = 81)
Lsc,1g = 0·206 + 0·267Vf (r = 0·967, n = 63)
Lsc,1.5g = 0·165 + 0·254Vf (r = 0·908, n = 101).
|
REFERENCES |
|---|
| TopAbstractIntroductionMethodsResultsDiscussionReferences |
|---|
| Cavagna, G. A. (1975). Force platforms as ergometers. Journal of Applied Physiology 39, 174-179 | [Medline] |
| Cavagna, G. A. & Franzetti, P. (1986). The determinants of the step frequency in walking in humans. The Journal of Physiology 373, 235-242 | [Abstract] |
| Cavagna, G. A., Franzetti, P. & Fuchimoto, T. (1983). The mechanics of walking in children. The Journal of Physiology 343, 323-339 | [Abstract] |
| Cavagna, G. A. & Margaria, R. (1966). Mechanics of walking. Journal of Applied Physiology 21, 271-278 | [Medline] |
| Cavagna, G. A., Saibene, F. & Margaria, R. (1963). External work in walking. Journal of Applied Physiology 18, 1-9. | |
| Cavagna, G. A., Thys, H. & Zamboni, A. (1976). The sources of external work in level walking and running. The Journal of Physiology 262, 639-657 | [Abstract] |
| Cavagna, G. A., Willems, P. A. & Heglund, N. C. (1998). Walking on Mars. Nature 393, 636. | |
| Coates, J. E. & Meade, F. (1960). The energy expenditure and mechanical energy demand in walking. Ergonomics 3, 97-119. | |
| Davis, B. L. & Cavanagh, P. R. (1993). Simulating reduced gravity: a review of biomechanical issues pertaining to human locomotion. Aviation Space and Environmental Medicine 64, 557-566 | [Medline] |
| Farley, C. T. & McMahon, T. A. (1992). Energetics of walking and running: insights from simulated reduced-gravity experiments. Journal of Applied Physiology 73, 2709-2712 | [Medline] |
| Fenn, W. O. (1930). Work against gravity and work due to velocity changes in running. American Journal of Physiology 93, 433-462. | |
| Fox, E. L., Bartels, R. L., Chaloupka, E. C., Klinzing, J. E. & Hoche, J. (1975). Oxygen cost during exercise in simulated subgravity environments. Aviation Space and Environmental Medicine 46, 300-303. | |
| Griffin, T. M., Tolani, N. A. & Kram, R. (1999). Walking in simulated reduced gravity: mechanical energy fluctuations and exchange. Journal of Applied Physiology 86, 383-390 | [Abstract/Full Text] |
| Heglund, N. C. (1981). A simple design for a force-plate to measure ground reaction forces. Journal of Experimental Biology 93, 333-338. | |
| Hewes, D. E., Spady, A. A. Jr & Harris, R. L. (1966). Comparative measurements of man's walking and running gaits on Earth and simulated lunar gravity. NASA Technical Note, TND-3363. | |
| Kram, R., Domingo, A. & Ferris, D. P. (1997). Effect of reduced gravity on the preferred walk-run transition speed. Journal of Experimental Biology 200, 821-826 | [Abstract] |
| McMahon, T. A. (1984). Muscles, Reflexes, and Locomotion, pp. 198-204. Princeton University Press, Princeton. | |
| Margaria, R. (1938). Sulla fisiologia e specialmente sul consumo energetico della marcia e della corsa a varie velocità ed inclinazioni del terreno. Atti Accademia nazionale Lincei Memorie 7, 299-368. | |
| Margaria, R. & Cavagna, G. A. (1964). Human locomotion in subgravity. Aerospace Medicine 35, 1140-1146. | |
| Newman, D. J. & Alexander, H. L. (1993). Human locomotion and work load for simulated lunar and mars environments. Acta Astronautica 29, 613-620. | |
| Newman, D. J., Alexander, H. L. & Webbon, B. W. (1994). Energetics and mechanics for partial gravity locomotion. Aviation Space and Environmental Medicine 65, 815-823 | [Medline] |
| Pletser, V. (1994). The aircraft parabolic flight microgravity programme of the European Space Agency. 45th IAF Congress, Jerusalem, October 1994; paper IAF/IAA-94-G.5.169. | |
| Rajulu, S. L., Klute, G. K. & Moore, N. R. (1992). A study to explore locomotion patterns in partial gravity environments. SAE Technical Paper Series, 22nd International Conference on Environmental Systems, Seattle, pp. 1-10. | |
| Willems, P. A., Cavagna, G. A. & Heglund, N. C. (1995). External, internal and total work in human locomotion. Journal of Experimental Biology 198, 379-393 | [Abstract] |
The authors would like to thank Professor Pietro Enrico di Prampero for his help at the beginning of this work. This study was supported by the European Space Agency, the Italian Ministero dell'Università e della Ricerca Scientifica e Tecnologica and the Belgian Fonds National de la Recherche Scientifique.
Corresponding author
G. A. Cavagna: Istituto di Fisiologia Umana, Via Mangiagalli 32, 20133 Milano, Italy.
Email: giovanni.cavagna{at}unimi.it
This article has been cited by other articles: (Search Google Scholar for Other Citing Articles)
|
|
 |
|
  F. Massaad, T. M. Lejeune, and C. Detrembleur The up and down bobbing of human walking: a compromise between muscle work and efficiency J. Physiol., July 15, 2007; 582(2): 789 - 799. [Abstract] [Full Text] [PDF] |
|
|
| |||||
|
|
.gif) |
|
 R. A. Ibrahim Excitation-Induced Stability and Phase Transition: A Review Journal of Vibration and Control, October 1, 2006; 12(10): 1093 - 1170. [Abstract] [PDF] |
|
|
| |||||
|
|
.gif) |
|
 R. L. Marsh, D. J. Ellerby, H. T. Henry, and J. Rubenson The energetic costs of trunk and distal-limb loading during walking and running in guinea fowl Numida meleagris: I. Organismal metabolism and biomechanics J. Exp. Biol., June 1, 2006; 209(11): 2050 - 2063. [Abstract] [Full Text] [PDF]
|
|
|
| |||||
|
|
|
|
G. A. Cavagna, N. C. Heglund, and P. A. Willems Effect of an increase in gravity on the power output and the rebound of the body in human running J. Exp. Biol., June 15, 2005; 208(12): 2333 - 2346. [Abstract] [Full Text] [PDF]
|
|
|
| |||||
|
|
.gif) |
|
 A. Lamontagne and J. Fung Faster Is Better: Implications for Speed-Intensive Gait Training After Stroke Stroke, November 1, 2004; 35(11): 2543 - 2548. [Abstract] [Full Text] [PDF]
|
|
|
| |||||
|
|
|
|
Y. P. Ivanenko, R. E. Poppele, and F. Lacquaniti Five basic muscle activation patterns account for muscle activity during human locomotion J. Physiol., April 1, 2004; 556(1): 267 - 282. [Abstract] [Full Text] [PDF] |
|
|
| |||||
|
|
.gif) |
|
 Y. P. Ivanenko, R. Grasso, V. Macellari, and F. Lacquaniti Control of Foot Trajectory in Human Locomotion: Role of Ground Contact Forces in Simulated Reduced Gravity J Neurophysiol, June 1, 2002; 87(6): 3070 - 3089. [Abstract] [Full Text] [PDF] |
|
|
| |||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| HOME | HELP | FEEDBACK | SUBSCRIPTIONS | ARCHIVE | SEARCH | TABLE OF CONTENTS |
) and to sustain the forward speed
changes (Wf; 
) are plotted as a function of walking
speed for the three gravity values. Note that at a given speed both
Wv and Wf increase with gravity, and
that the speed at which Wv equals Wf
also increases with gravity. Lines are fitted through all the data,
using a third-order polynomial fit for Wv at 1·5 and
1·0 g, a second-order polynomial fit for Wv at
0·4 g, and a linear fit for Wf (KaleidaGraph
3.08d). Other indications are as in Fig. 5. 
) and 1·5 g (